Aufgabenstellung:
An einem Transformator mit dem Übersetzungsverhältnis (Windungsverhältnis)
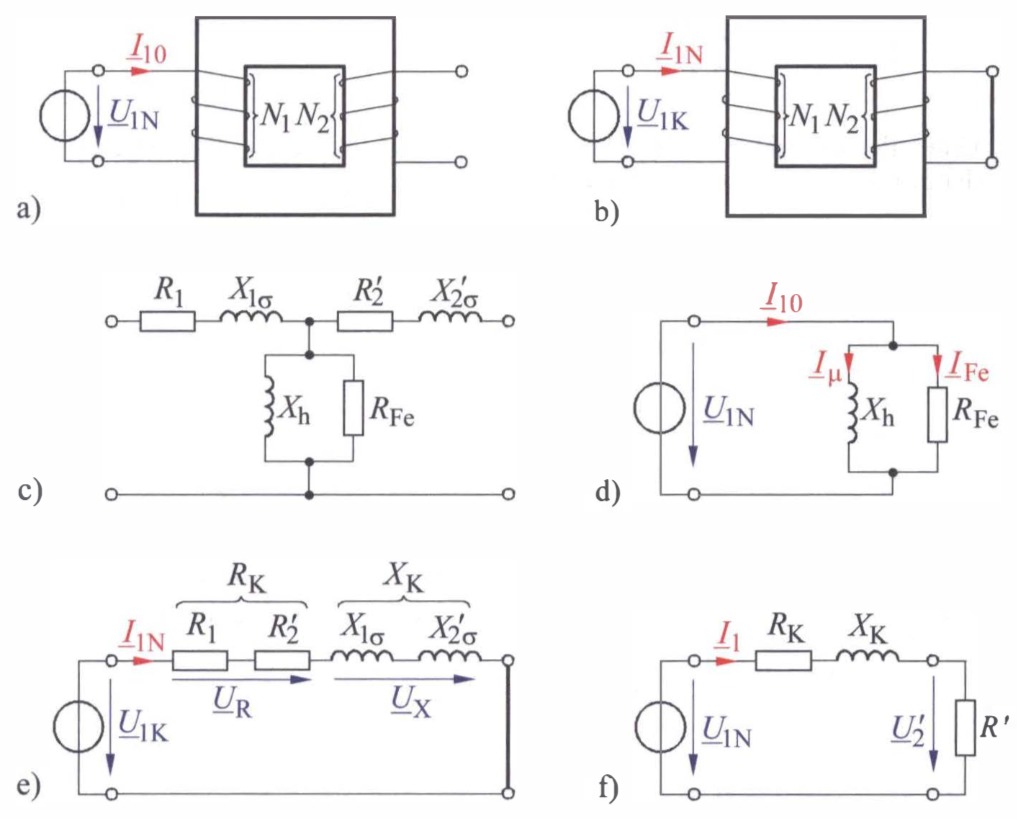
Abbildungen zur Ermittlung der Größen des Ersatzschaltbildes eines Transformators.
Beim Leerlaufversuch nach Abbildung (a) wird die Primärwicklung - bei geöffnetem Sekundärkreis - an Nennspannung gelegt. (Anmerkung: Die Nennspannung ist die jenige Spannung, für die der Transformator ausgelegt worden ist.)
Anschließend wird ein Kurzschlussversuch durchgeführt.
a) Es sind die Größen des in Abbildung (c) dargestellten Ersatzschaltbildes des Transformators zu bestimmen.
b) Wie groß sind der ohmsche Widerstand
c) Wie groß ist die Sekundärspannung
Lösungsweg:
a) Transformator Größen
Beim leerlaufenden Transformator können wir wegen
Darin gilt
Weiterhin geht aus Abbildung (d) hervor, dass
ist.
Damit erhalten wir aus Abbildung (d) für den Hauptblindwiderstand
und für den Eisenverlustwiderstand
Beim kurzgeschlossenen Transformator gilt wegen
Darin ist
Weiterhin geht aus Abbildung (e) hervor, dass
ist.
Damit erhalten wir aus Abbildung (e)
Unter Berücksichtigung der Annahmen
und der primärseitige Streublindwiderstand als
b) Ohmscher Widerstand und Streublindwiderstand
Zur Ermittlung des sekundärseitigen ohmschen Wicklungswiderstandes
Dadurch finden wir die Ergebnisse
c) Sekundärspannung
Zur Berechnung der gesuchten Ausgangsspannung des belasteten Transformators können wir - wie vorgegeben - die Widerstände
Somit gilt das in Abbildung (f) dargestellte (vereinfachte) Ersatzschaltbild.
Darin stellt
Hierbei ergibt sich
Damit gilt in Abbildung (f) nach der Spannungsteilerregel
Wir rechnen diesen Wert auf die Sekundärseite um und erhalten dadurch das gesuchte Ergebnis
Lösung:
siehe Lösungsweg