2 / 10

Aufgabenstellung:

Gegeben sind zwei harmonische Zeitfunktionen

Bekannt sind die Amplituden und A sowie die Frequenz .

a) Zeichnen Sie den zeitlichen Verlauf beider Funktionen über eine Periode für die Fälle:
1)

2)

3)

b) Welchen Bauteilen entspricht die Phasenverschiebung in den eben genannten Fällen?

c) Zeichnen Sie den zeitlichen Verlauf der Funktion für die oben genannten Fälle.

d) Berechnen Sie den arithmetischen Mittelwert

allgemein und für die Werte:
1)

2)
3)

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Funktionsgraphen

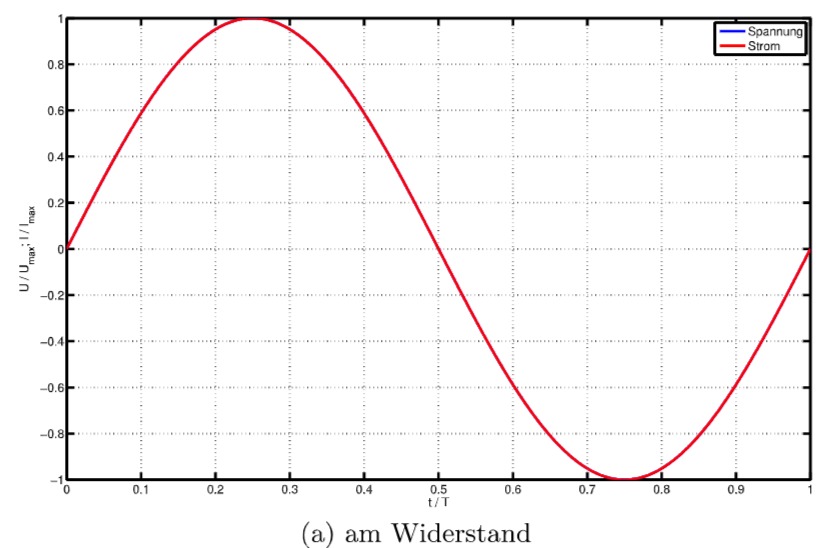
1)

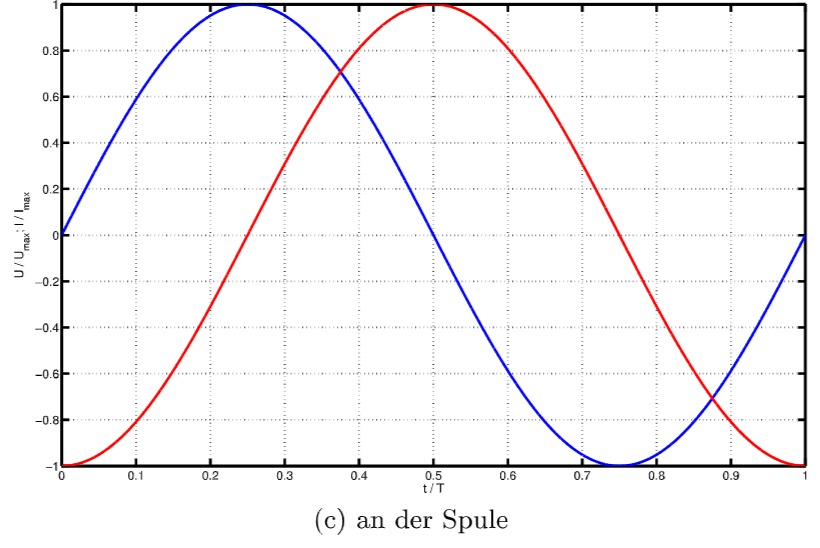
Abbildung

2)

Abbildung

3)

Abbildung

b) Bauteile

1) einem Widerstand: Strom und Spannung sind in Phase

2) einer Kapazität: Am Kondensator eilt der Strom der Spannung um bzw. um voraus.

3) einer Induktivität: An einer Spule eilt die Spannung dem Strom um bzw. um voraus.

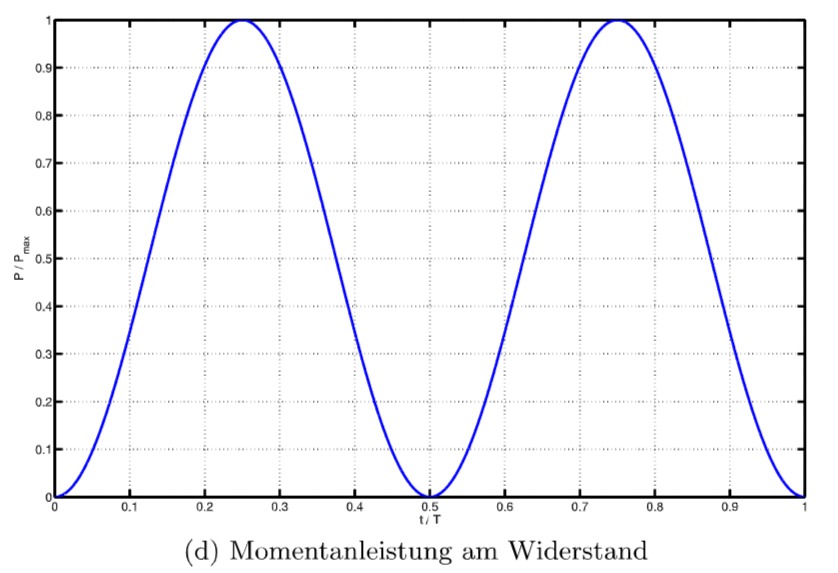
c) Verlauf der Momentanleistung

1)

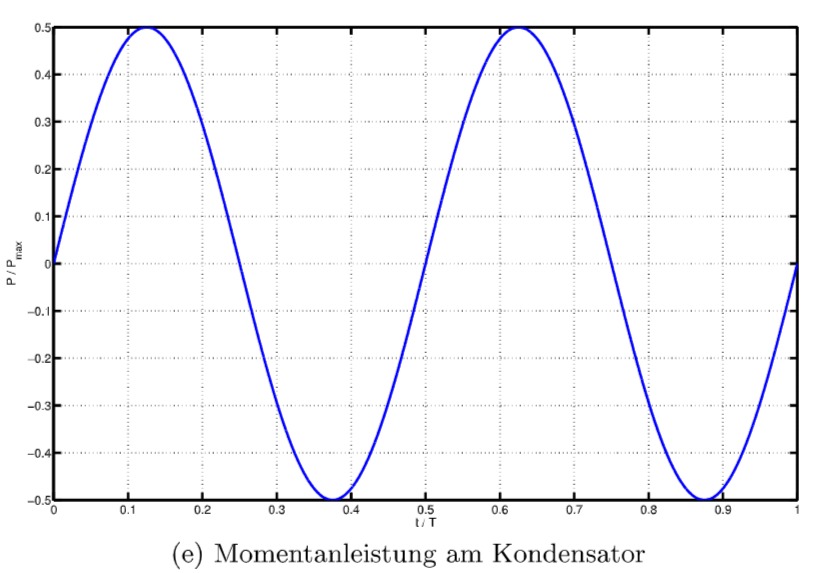
Abbildung

2)

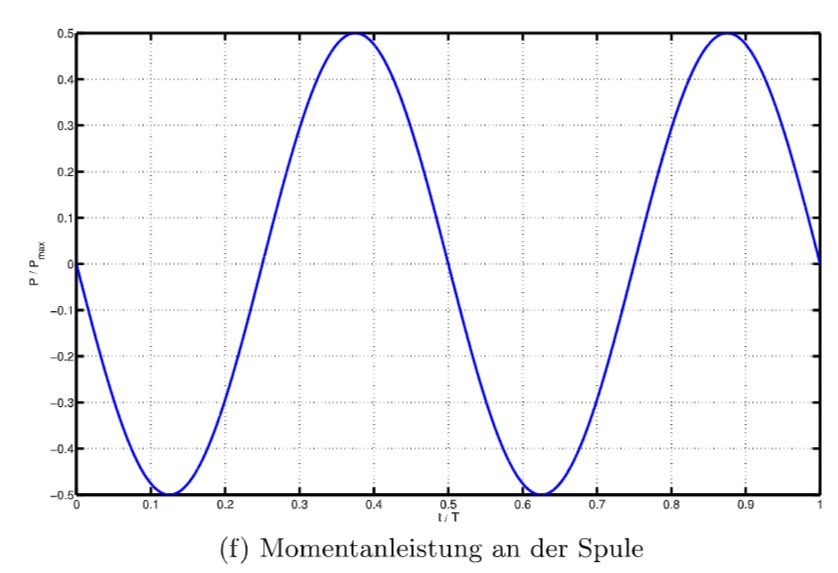
Abbildung

3)

Abbildung

c) Berechnung des arithmetischen Mittelwerts

Ansatz: Einsetzen der Zeitfunktion für Spannung und Strom in Gleichung

Mit Hilfe des Additionstheorems

wird (setze und

Eingesetzt gilt dann

Das Integral einer Sinus- oder Kosinusfunktion über eine vollständige Periode ist immer Null und übrig bleibt

Damit wird die allgemeine Lösung

1)

2)

3) :

Lösung:

siehe Lösungsweg