Aufgabenstellung:
- Auf welcher Kraftwirkung beruht der Halleffekt? Erläutern Sie den Halleffekt!
- Ein dünnes Halbleiterplättchen befindet sich gemäß Abbildung 1 senkrecht zum Magnetfeld und wird von einem Strom
durchflossen. Bestimmen Sie die Hallspannung - Bestimmen Sie die Hallspannung
unter der Voraussetzung eines Winkels zwischen Magnetfeld und Oberfläche des Hallplättchens, wie in Abbildung 2 gezeigt. - Gegeben sei ein unendlich langer Leiter mit verschwindendem Durchmesser. Der Leiter werde von einem Strom von
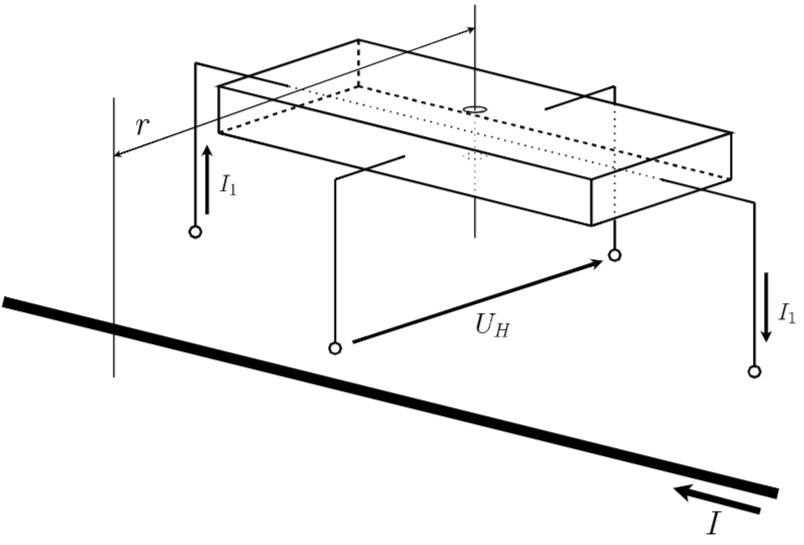
durchflossen. Zur Messung der magnetischen Induktion werde ein Hallplättchen senkrecht zur Feldrichtung verwendet (Abb. 3). Wie groß ist die Hallspannung in Abhängigkeit des Abstandes zum Leiter?
Wozu könnte man eine solche Messung in der Praxis nutzen?
Abbildung 1: Halleffekt bei senkrechtem Magnetfeld:
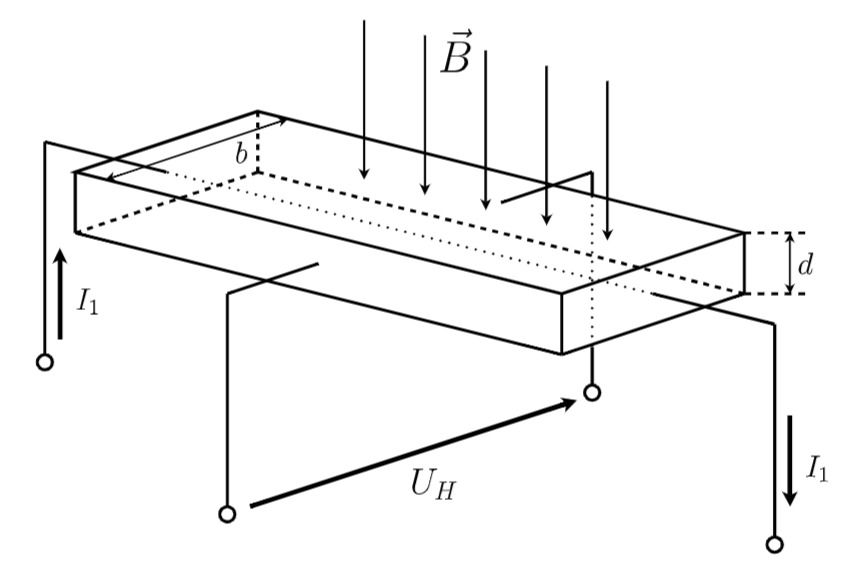
Abbildung 2: Halleffekt bei schrägem Magnetfeld
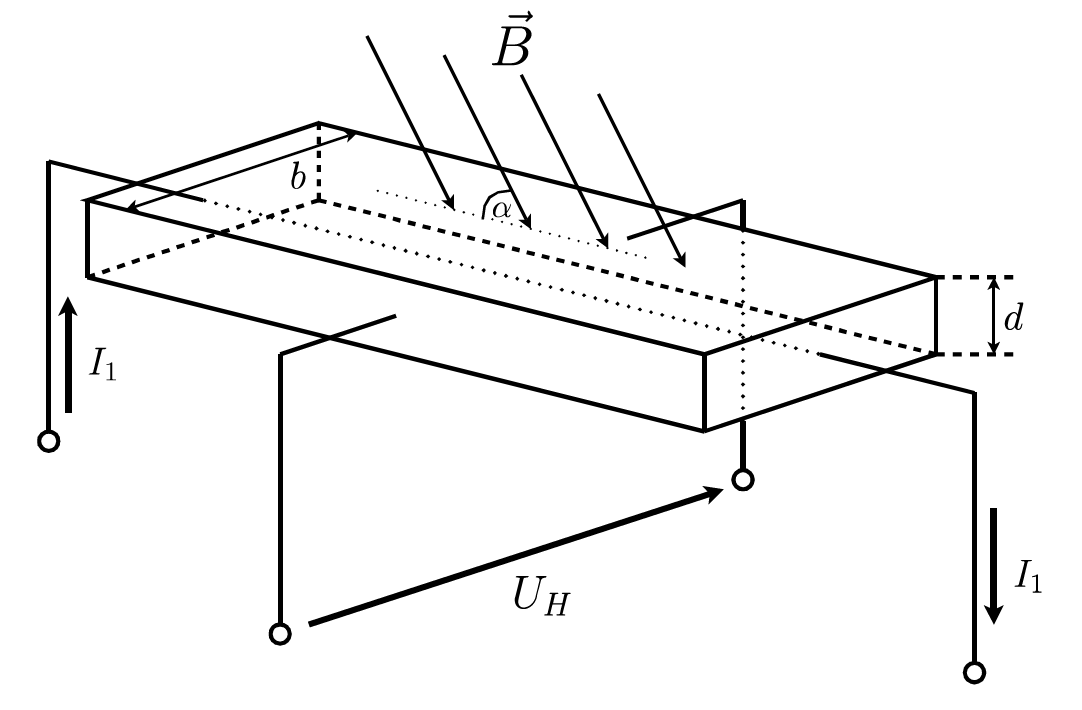
Abbildung 3: Halleffekt bei Feld aus parallel laufendem Leiterstrom
Bemerkung: Die magnetische Induktion kann als konstant über der gesamten Breite des Plättchens angesehen werden.
Gegeben sind die folgenden Werte:
Lösungsweg:
Aufgabenteil a)
- Ladungsträger (Elektronen oder Löcher, je nach Halbleitermaterial) bewegen sich aufgrund des Stromflusses mit der Geschwindigkeit
im Leiter - Auf sie wirkt aufgrund des
-Feldes die Lorentzkraft, die die Elektronen auf eine Seite des Plättchens zieht - Durch die Ladungsakkumulation ergbit sich ein elektrisches Feld
, so dass beide Krafte begtragsgleich aber unterschiedlich gerichtet sind: - Die somit entstehende Spannung
wird an der Seite des Plättchens abgegriffen und ist ein Maß für die Stärke des -Feldes. Sie wird daher als Hallspannung bezeichnet.
Aufgabenteil b)
Der Ansatz für diese Aufgabe ist das Gleichgewicht der Coulomb'schen Kraft und der Lorentzkraft. Die Ursachen der Kräfte sind verschieden:
- Coulomb'sche Kraft: Anwesenheit von Ladung
- Lorentzkraft: Bewegte Ladung im Magnetfeld
Sie sind gegeben als:
Ansatz:
Nun bleibt noch die Geschwindigkeit
- der Stromfluss im Halbleiterplättchen kann als homogen über die Querschnittsfläche betrachtet werden
- im (raumladungsfreien) Halbleiter befinden sich aufgrund der Struktur immer gleich viele Ladunsgträger
- ein Strom ist die Änderung der Ladung nach der Zeit:
- eine Geschwindigkeit ist die Änderung des Ortes nach der Zeit:
Änderung der Ladung nach der Zeit:
mit
-
-
-
-
Die Änderung des Volumens
dV einsetzen ergibt:
Ladungsträger eingesetzt
Es ergibt sich für das elektrische Feld:
Die daraus resultierende Hallspannung bestimmt sich aus dem Integral
In unserem Fall also
Aufgabenteil c)
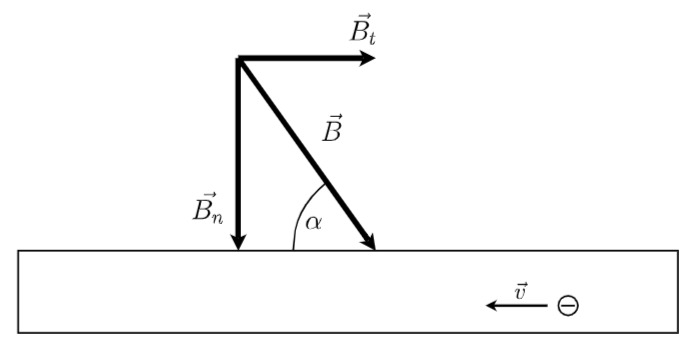
Im Hallplättchen werden die Elektronen nur von der rechtwinklig zur Geschwindigkeit
Der Betrag der Flussdichte ist nun also gegeben durch:
Abbildung 4: Normalkomponente der magn. Flussdichte:
Daraus folgt für die Hallspannung:
Aufgabenteil
Die Hallspannung wird durch die magnetische Flussdichte aufgebaut. Sie lässt sich mit dem Durchflutungsgesetz angeben.
Die Variable
Als Praxisbezug kann man hier eine mögliche Anwendung (z. B. Stommessung ohne die Leitung aufzutrennen) dieser Messung angeben.
Lösung:
- siehe Text.