Schaltvorgänge in RL- und RC-Schaltungen - Ohmsch-induktiver Wechselst

2 / 3

Aufgabenstellung:

In der Schaltung nach Bild a wird die Reihenschaltung einer Spule mit der Induktivität und des Wirkwiderstände an eine Spannungsquelle angeschlossen. Diese liefert eine (sinusförmige) Wechselspannung mit dem Scheitelwert und der Frequenz . Der Schalter wird im positiven Nulldurchgang der Spannung geschlossen.

Es ist der zeitliche Verlauf des Stromes zu ermitteln und grafisch darzustellen. (Der Schaltzeitpunkt entspreche dem Zeitpunkt .)

Bild : Anlegen einer Spule mit Reihenwiderstand an Wechselspannung.

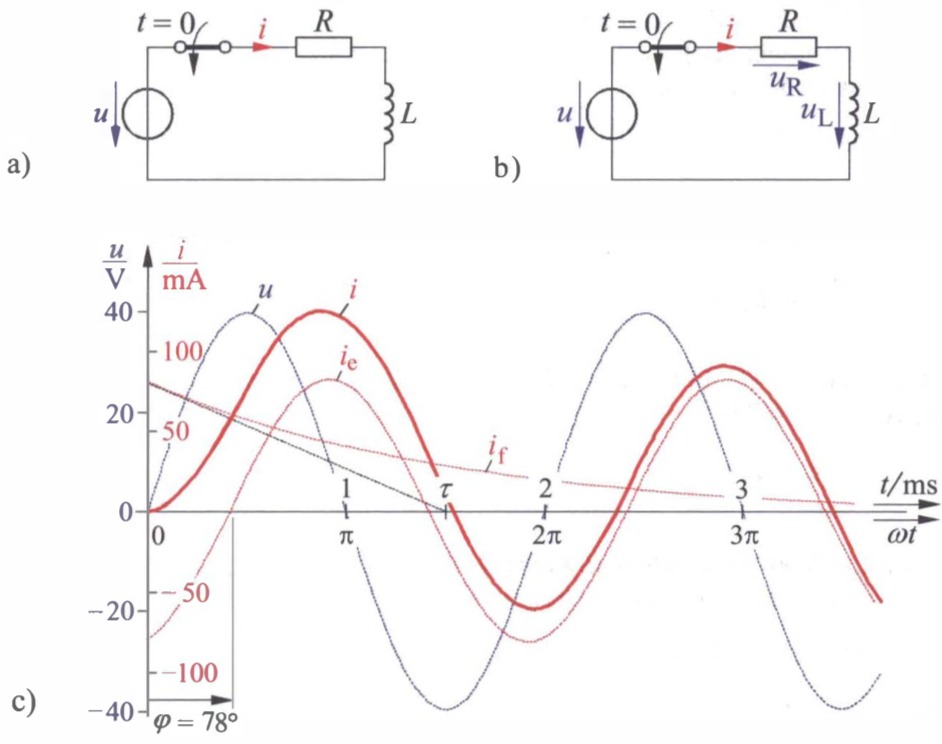
Abbildung

a) Gegebene Schaltung,
b) Schaltung mit eingetragenen Spannungen, c) zeitlicher Verlauf des Stromes (als Überlagerung des stationären Stromes und des freien Stromes ) sowie zeitlicher Verlauf der Spannung

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

Wir führen nach Bild b die Spannungen und ein. In der Schaltung gilt

Hierbei können wir die anliegende sinusförmige Wechselspannung durch

darstellen. Bei dieser Darstellung wird berücksichtigt, dass der Stromkreis im positiven Nulldurchgang von (dieser Nulldurchgang entspricht dem Zeitpunkt ) geschlossen wird. Mit und ergibt sich:

Zur Lösung dieser Differenzialgleichung zerlegen wir den gesuchten Strom in den (sich einstellenden) stationären Strom und den (vorübergehend auftretenden) freien Strom also in

Da der nach dem Schließen des Schalters auftretende Strom in den stationären Strom übergeht, muss gelten. Deshalb ist

Durch Subtrahieren erhalten wir:

Den stationären Strom können wir nach den für sinusförmige Vorgänge bekannten Verfahren ermitteln. Der Strom hat bei dem Spulen-Blindwiderstand

folglich den Scheitelwert

und eilt der anliegenden Wechselspannung um den Phasenverschiebungswinkel

nach. Damit lautet die Gleichung für den zeitlichen Verlauf des stationären Stromes

Verwende die Lösung:

Dabei ist eine noch zu bestimmende Konstante. Die Größe

stellt die Zeitkonstante dar. Einsetzen ergibt

Die hierin enthaltene Konstante erhalten wir aus der Überlegung, dass sich der Strom infolge der vorhandenen Induktivität nicht sprunghaft ändem kann. Es muss somit in Bild b bei auch sein. Verwenden wir diese fangsbedingung, so finden wir

Hieraus folgt mit

Damit lautet die endgültige Lösung für den gesuchten Strom:

Hierbei ist die Kreisfrequenz der Wechselspannung. Den zeitlichen Verlauf des Stromes - als Überlagerung des stationären (sinusförmigen) Stromes und des freien (nach einer e-Funktion abklingenden) Stromes - zeigt Bild c. Ebenfalls eingetragen ist der zeitliche Verlauf der Wechselspannung . Deren Periodendauer beträgt