Aufgabenstellung:
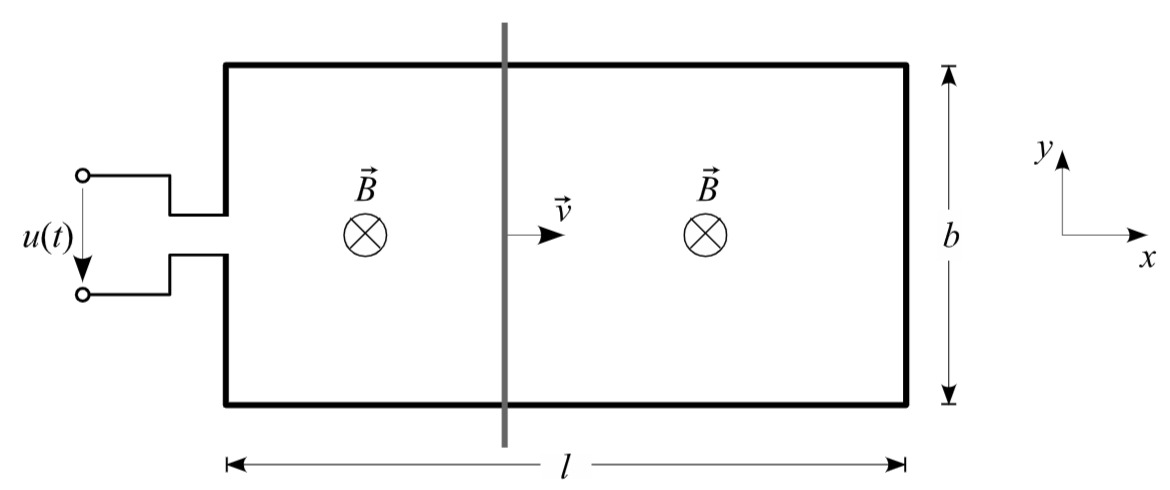
Ein Stab gleitet gemäß der Abbildung auf einer Schiene mit der Geschwindigkeit
Berechnen Sie für das Zeitintervall
Hinweis:
Die Rückwirkung des induzierten Stroms ist bei der Berechnung zu vernachlässigen.
Lösungsweg:
Spannung
Der Stab unterteilt die durch die Schiene begrenzte rechteckige Fläche in zwei Teile. Dadurch, dass sich der Stab bewegt, werden die Flächen in ihrer Größe verändert, was zu einer Änderung des sie durchsetzenden magnetischen Flusses führt. Durch die Flussänderung wiederum werden entlang der beiden Flächenberandungen Spannungen induziert. Die rechte der beiden Berandungen besteht vollständig aus leitendem Material, so dass dort auch ein Umlaufstrom induziert wird.
Im ersten Schritt berechnen wir die beiden magnetischen Flüsse
Für die beiden magnetischen Flüsse ergibt sich
Wir benötigen die magnetischen Flüsse als Funktion der Zeit und nicht als Funktion des Ortes. Deshalb muss in den Gleichungen (1) und (2) die Variable
und
Um die beiden Umlaufspannungen
Die zur Fläche
In der linken Masche fließt kein Strom, so dass in den Schienenabschnitten die Stromdichte und damit auch die elektrische Feldstärke gleich Null ist. Mit Hilfe eines Maschenumlaufes für die Umlaufspannung
Jetzt muss Gleichung (5) nur noch nach