Aufgabenstellung:
Zwei lange, gerade, parallel verlaufende Leiter nach Bild 5.6a mit einem gegenseitigem Abstand von
Wie groß ist die im Punkt P vorhandene magnetische Feldstärke
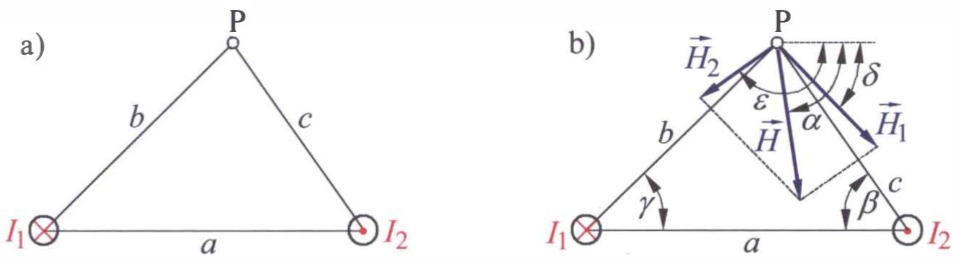
a) Gegebene Anordnung,
b) von den Strömen im Punkt P erzeugte Feldstärkekomponenten und deren vektorielle Addition
Lösungsweg:
Die gesuchte Feldstärke ermitteln wir durch Überlagerung (vektorielle Addition) der von den einzelnen Strömen verursachten Feldstärkekomponenten. Der Strom
Im Punkt P verläuft dieses Feld somit senkrecht zur Linie
Der Vektor dieser Feldstärke
Der zugehörige Feldstärkevektor
Dazu bestimmen wir in Bild
Durch Anwendung des Kosinussatzes
finden wir, wenn wir die Gleichung nach
Entsprechend wird
Damit erhalten wir für die in Bild b eingetragenen Winkel
Zur Addition der Feldstärkevektoren
Dazu stellen wir
Die gesuchte Gesamtfeldstärke
und mit der Linie
einschließt.