Aufgabenstellung:
Zwei Rohre aus Metall sind nach Bild a koaxial angeordnet. Von dem inneren Rohr sind die Radien
Es ist die magnetische Feldstärke
Zur Bestimmung der magnetischen Feldstärke in der Umgebung und im lnnern koaxial angeordneter, stromführender Rohre:
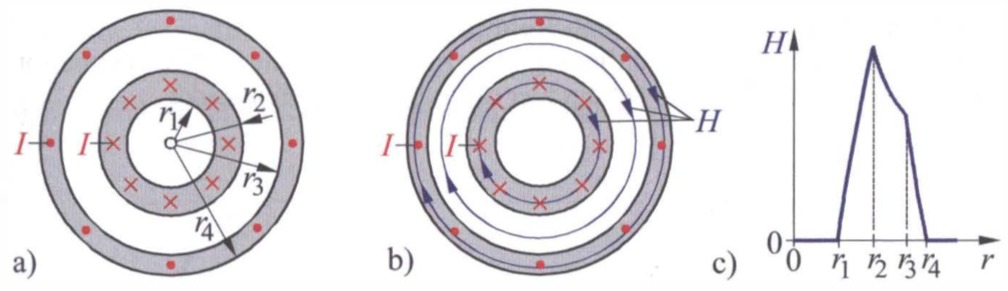
a) Gegebene Anordnung
b) Verlauf des magnetischen Feldes
c) Darstellung der Abhängigkeit der magnetischen Feldstärke
Lösungsweg:
Die auftretenden magnetischen Feldlinien bilden nach Bild b im Uhrzeigersinn verlaufende konzentrische Kreise. Die gesuchte magnetische Feldstärke erhalten wir dadurch, dass wir die jeweils vorhandene Durchflutung
Dabei können wir fünf verschiedene Bereiche unterscheiden.
1. Bereich, Innenraum des inneren Rohres
In diesem Bereich ist die Durchflutung aller (konzentrischen) Kreise gleich Null. Das bedeutet, dass hier kein magnetisches Feld existiert, also
2. Bereich, Mantel des inneren Rohres
Im Mantel des inneren Rohres herrscht die Stromdichte
Daher beträgt die Durchflutung eines Kreises (einer Feldlinie) mit dem Radius
Hiermit ergibt sich für die magnetische Feldstärke im Rohrmantel
3. Bereich, Raum zwischen beiden Rohren
In diesem Bereich ist die Durchflutung aller Kreise (Feldlinien) gleich dem Strom
4. Bereich, Mantel des äußeren Rohres (
Im Mantel des äußeren Rohres herrscht die Stromdichte
Somit beträgt in diesem Raum die Durchflutung eines Kreises (einer Feldlinie) mit dem Radius
Daher erhalten wir die in diesem Bereich vorhandene magnetische Feldstärke als
5. Bereich, Raum außerhalb des äußeren Rohres
In diesem Bereich ist die Durchflutung aller Kreise gleich Null. Hier existiert also kein magnetisches Feld, so dass
In Bild
Lösung:
siehe Lösungsweg