9 / 9

Aufgabenstellung:

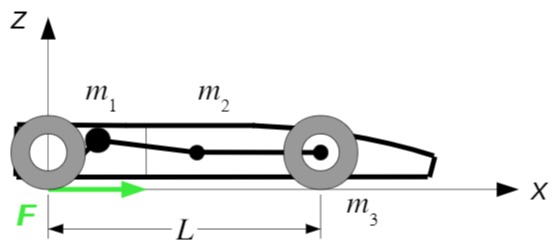AbbildungDas Ersatzmodell eines Rennwagens besteht aus drei starr miteinander verbundenen Punktmassen, die starr mit dem Radaufstandspunkt des Hinterrads verbunden sind. Die starren Verbindungen werden als masselos betrachtet.

Der Rennwagen wird durch eine an den Hinterrädern angreifende Kraft beschleunigt.

  1. Wie groß ist die Beschleunigung des Rennwagens?
  2. Wie groß sind die Vertikalkräfte an den Rädern?
  3. Wie groß muss der Haftungskoeffizient zwischen Reifen und Fahrbahn mindestens sein, damit die Hinterräder nicht durchdrehen?

Gegeben:

Massen:

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Beschleunigung

Die einzige in -Richtung auf das Massenpunktsystem wirkende äußere Kraft ist die Antriebskraft .

Aus dem Schwerpunktsatz folgt

Dabei ist die Gesamtmasse des Rennwagens.

Zahlenwerte:

b) Vertikalkräfte

Die gesuchten Vertikalkräfte und können aus dem Kräftegleichgewicht in z-Richtung und dem Drallsatz um Punkt berechnet werden.

Kräftegleichgewicht in z-Richtung:

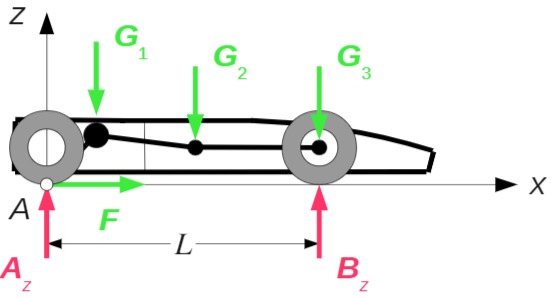
Abbildung

Die - Achse zeigt in die Zeichenebene. Da alle drei Massenpunkte starr miteinander verbunden sind, bewegen sie sich mit der gleichen Geschwindigkeit.

Für die -Komponente des Dralls um den Punkt gilt daher:

Der Bezugspunkt bewegt sich mit der gleichen Geschwindigkeit wie der Schwerpunkt. Daher gilt . Der Drallsatz bezüglich des bewegten Bezugspunkts A vereinfacht sich somit zu

In Komponenten lautet diese Gleichung

Mit aufgestellten Schwerpunktskoordinaten folgt für

Die Vertikalkraft im Punkt A berechnet sich damit zu

Zahlenwerte:

c) Haftungskoeffizient

Aus der Haftbedingung folgt 

Zahlenwert:

Lösung:

  2. Vertikalkräfte hinten:
    Vertikalkräfte vorne: