Aufgabenstellung:
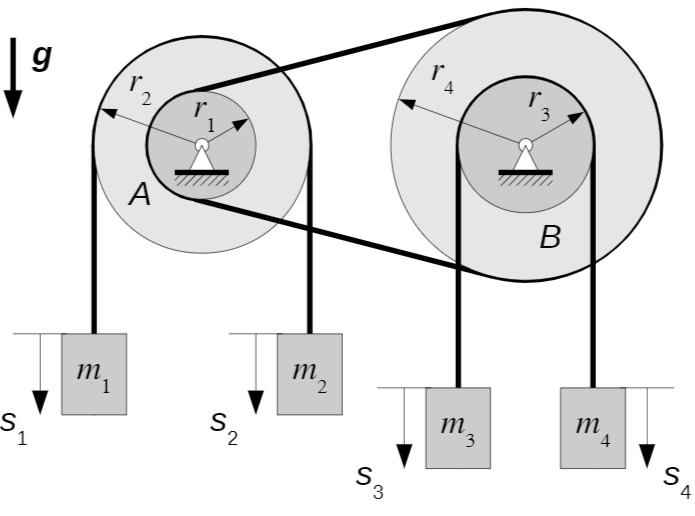 Die beiden Rollen
Die beiden Rollen
Über den äußeren Umfang der Rolle
Über den inneren Umfang der Rolle
Die Rollen, die Seile und der Riemen sind masselos.
- Geben Sie die Lagekoordinaten
und in Abhängigkeit von der Lagekoordinaten an. - Ermitteln Sie die Beschleunigungen
und der Massen. - Ermitteln Sie die Seilkräfte
bis in den Seilen, an denen die Massen hängen.
Hinweis zu b): Verwenden Sie die Momentengleichgewichtsbedingungen für die beiden Rollen, um die Kräfte im Riemen zu eliminieren, und die Bewegungsgleichungen für die vier Massen, um die Seilkräfte zu eliminieren.
Gegeben:
Lösungsweg:
a) Kinematische Beziehungen
Als Hilfsgrößen werden die Winke
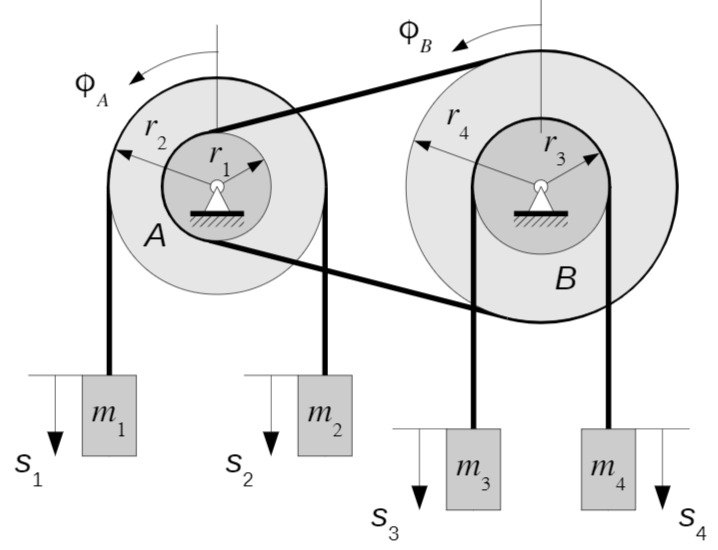
Es folgt für die gesuchten Größen:
b) Beschleunigungen
Bewegungsgleichungen der Massen:
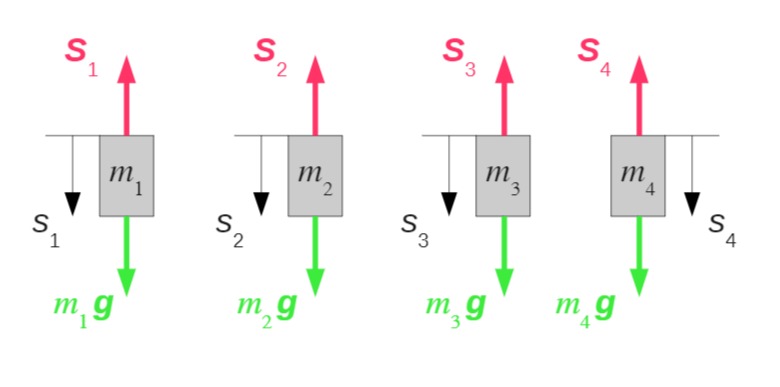
Da die Rollen masselos und reibungsfrei gelenkig gelagert sind, muss für sie das Momentengleichgewicht erfüllt sein:
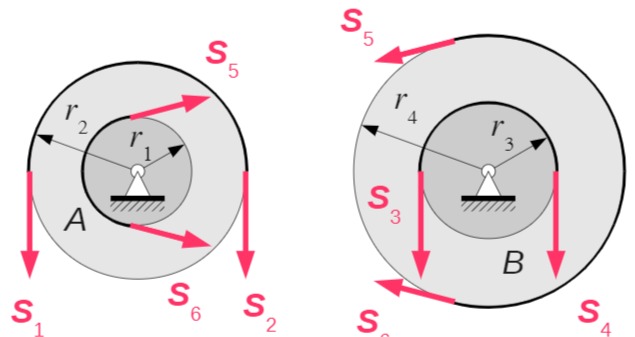
Addition der beiden aus dem Momentengleichgewicht gewonnenen Beziehungen ergibt:
Aus den Bewegungsgleichungen folgt für die Seilkräfte:
Einsetzen in die obige Gleichung führt auf:
Mit den kinematischen Beziehungen folgt daraus eine Gleichung für die Beschleunigung
Die übrigen Beschleunigungen können nun aus den kinematischen Beziehungen berechnet werden:
Zahlenwerte:
c) Seilkräfte