Aufgabenstellung:
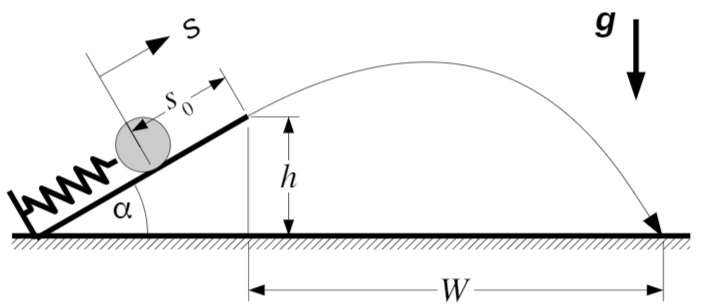 Auf einem Katapult befindet sich eine Kugel der Masse
Auf einem Katapult befindet sich eine Kugel der Masse
Für die Kraft, die die Feder auf die Kugel ausübt, gilt:
Während der Beschleunigung gleitet die Kugel auf dem Katapult. Der Reibungskoeffizient zwischen Kugel und Katapult ist
- Mit welcher Geschwindigkeit
verlässt die Kugel das Katapult? - Wie groß ist die Wurfweite
Gegeben:
Lösungsweg:
a) Abschussgeschwindigkeit
Skizze aller angreifenden Kräfte:
An der freigeschnittenen Kugel greifen die Federkraft

Bewegungsgleichungen aufstellen:
Gleitreibungsgesetz:
Federkraft:
Einsetzen der Kräfte in die Bewegungsgleichung in s-Richtung ergibt
Daraus folgt für die Beschleunigung:
Mit den Abkürzungen
gilt:
Die Beschleunigung ist ortsabhängig. Da die Anfangsgeschwindigkeit null ist, berechnet sich die Geschwindigkeit
Zahlenwerte:
b) Wurfweite
Der Ursprung des Koordinatensystems für die Wurfparabel wird in den Punkt gelegt, an dem die Kugel das Katapult verlässt (Skizze):
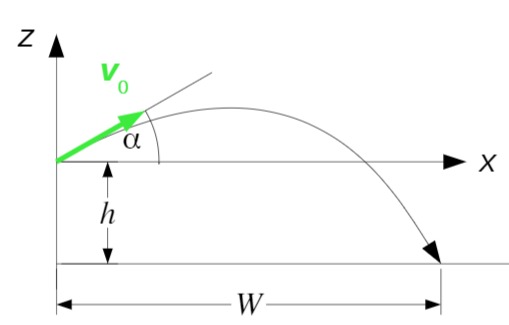
Dann gilt für die Wurfweite:
Daraus folgt für
Von den beiden Lösungen ist nur die Lösung
Zahlenwert: