Aufgabenstellung:
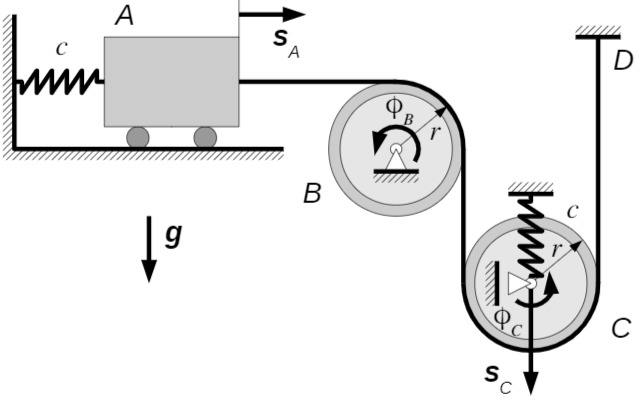 Das abgebildete System besteht aus dem Wagen
Das abgebildete System besteht aus dem Wagen
Die Rolle
Der Wagen
Am Wagen
In der dargestellten Lage sind beide Federn entspannt, und das System ist in Ruhe.
- Geben Sie die Verschiebung
des Wagens sowie die Drehwinkel und der Rollen und in Abhängigkeit von der Verschiebung der Rolle C an. - Ermitteln Sie mithilfe des Energieerhaltungssatzes die Geschwindigkeit
der Rolle in Abhängigkeit von der Verschiebung - Ermitteln Sie die Beschleunigung
der Rolle in Abhängigkeit von der Verschiebung . - Mit welcher Kreisfrequenz w schwingt das System um die statische Gleichgewichtslage?
Gegeben:
Lösungsweg:
a) Kinematik
Rolle
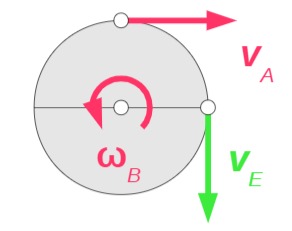
Rolle B:
b) Geschwindigkeit der Rolle
Als Nullniveau für die Lageenergie der Rolle
Für eine beliebige ausgelenkte Lage gilt:
Feder am Wagen
Wagen
Rolle
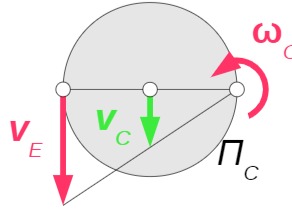
Rolle C:
Feder an Rolle C:
Der Energieerhaltungssatz lautet:
Mit den kinematischen Beziehungen folgt:
Mit den Beziehungen für die Massen und Massenträgheitsmomente folgt für
c) Beschleunigung der Rolle
d) Kreisfrequenz
Aus der Schwingungsgleichung
kann abgelesen werden: