Aufgabenstellung:
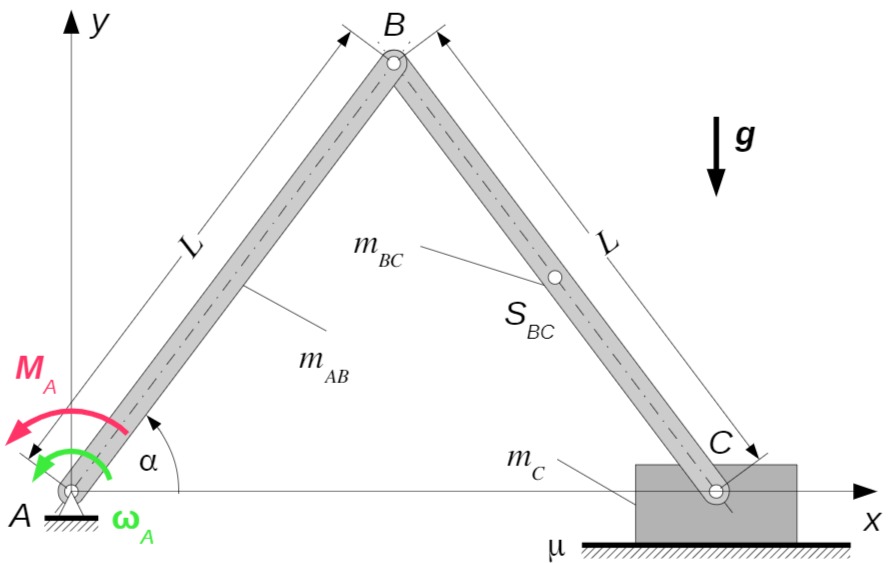
Die beiden dünnen homogenen Stäbe
Der Stab
- Bestimmen Sie zeichnerisch die Lage des Momentanpols des Stabs
. Lesen Sie daraus eine Beziehung für seine Winkelgeschwindigkeit ab (positiv im Gegenuhrzeigersinn). - Bestimmen Sie den zeitlichen Verlauf der Koordinaten
und des Schwerpunkts des Stabs sowie der Koordinate von Punkt . Leiten Sie daraus Beziehungen für die Beschleunigungen sowie ab. - Stellen Sie alle kinetischen Gleichungen auf, die zur Bestimmung des Antriebsmoments
benötigt werden. Die Gleichungen müssen nicht aufgelöst werden.
Gegeben:
Lösungsweg:
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen
a) Momentanpol und Winkelgeschwindigkeit
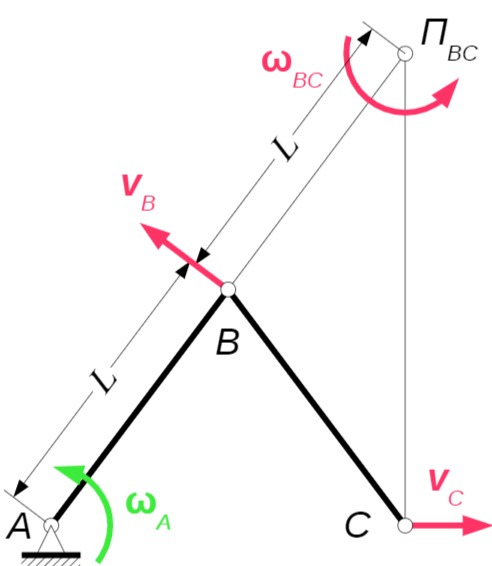
Es gilt:
b) Koordinaten und Beschleunigungen
Schwerpunkt von Stab
c) Kinetische Gleichungen
Stab
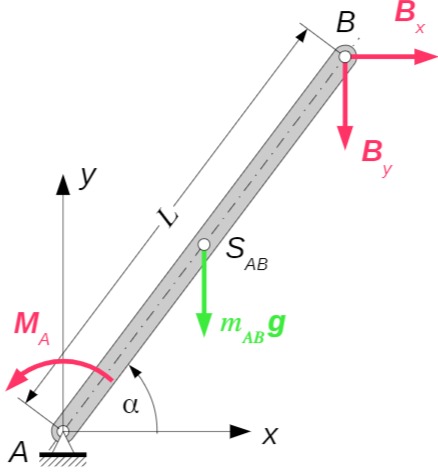
Stab
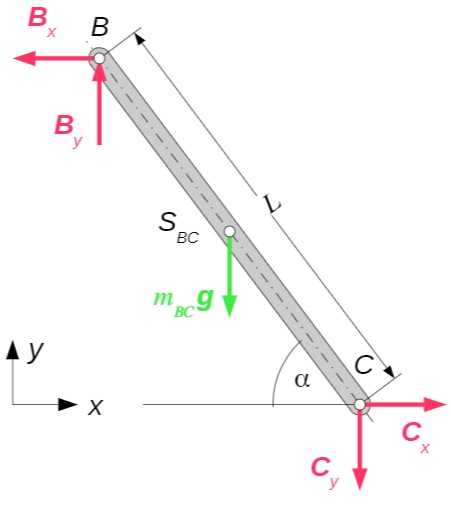
Klotz C:
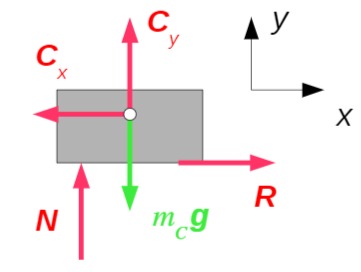
Reibungsgesetz:
Lösung:
Siehe Lösungsweg.