8 / 16

by Manfred Strohrmann

(H.ErT.Z-Online)

Aufgabenstellung:

Der dargestellte Schaltungsaufbau mit zwei idealen Operationsverstärkern stellt eine spannungsgesteuerte Stromquelle dar.

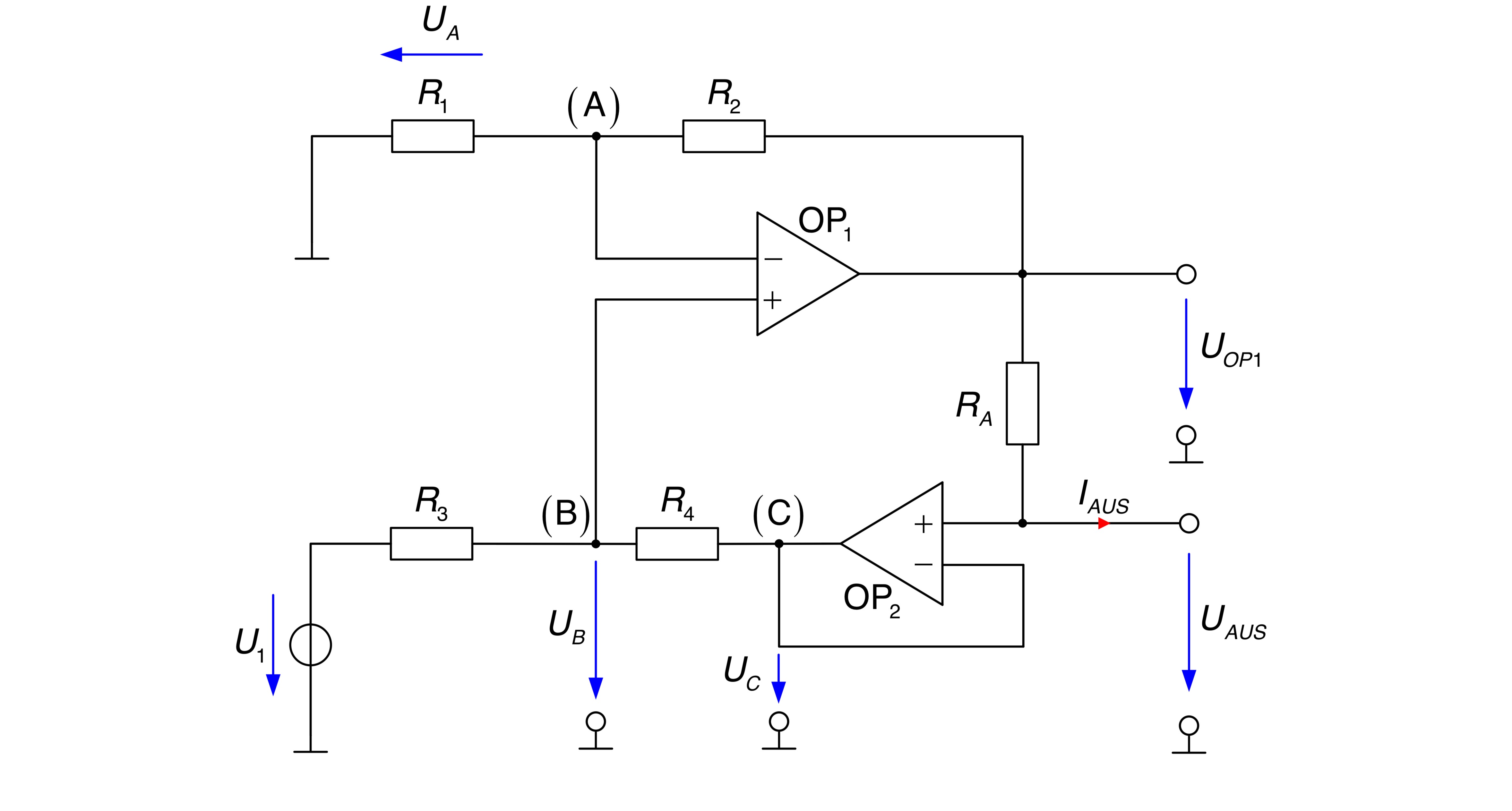
Abbildung

  1. Geben Sie die Übertragungsfunktion an und zeigen Sie, dass der Ausgangsstrom unabhängig von der Ausgangsspannung ist.
  2. Dimensionieren Sie die Schaltung mit den folgenden Randbedingungen:
1

2

3
4

Die Versorgungsspannung der OPs sei d.h. die Ausgansspannung der OPs bewegt sich zwischen und

5  Die Widerstände bis sollen maximal groß sein.

Hinweis:
Im Interesse eines kleinen Fehlers wird der Spannungsabfall über so groß wie möglich gewählt, ohne die Operationsverstärker in die Sättigung zu treiben.

Lösungsweg:

Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen

a) Bestimmen der Übertragungsfunktion

  • In die Schaltung werden alle für die Berechnung relevanten Zählpfeile eingetragen.

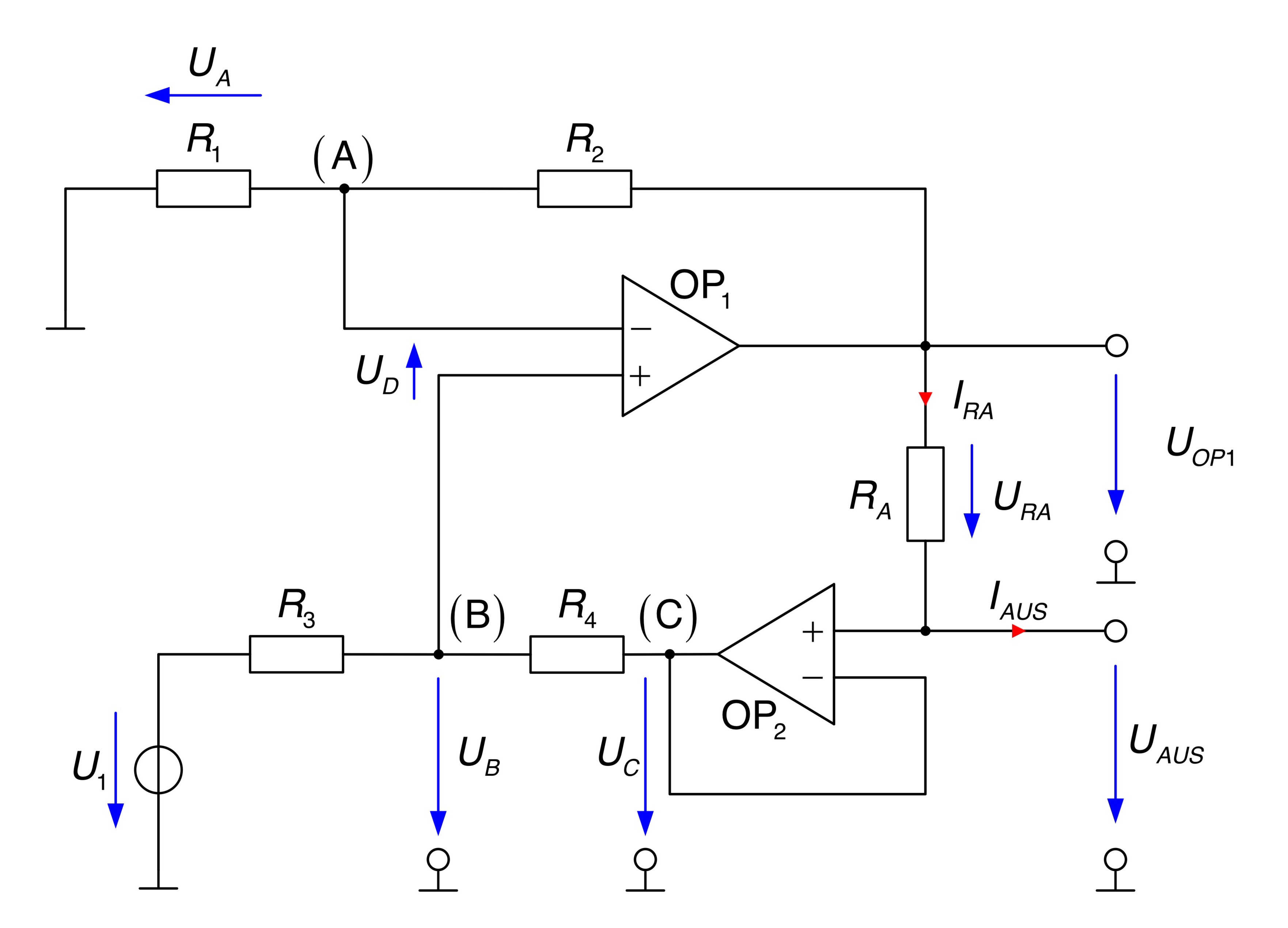
Abbildung

Der Operationsverstärker OP wird als idealer Spannungsfolger eingesetzt.

Dementsprechend gilt:

Des Weiteren kann eine Masche über die Knoten (A) und (B) gelegt werden.

Die Gleichung lautet:

Mit der Bedingung    ist  

Die Größen und sollen im nächsten Schritt ersetzt werden.

Die Spannung berechnet sich nach der Spannungsteilerregel mit den Größen und .

Der Ausgang des Operationsverstärkers kann als ideale Spannungsquelle betrachtet werden.

Mittels Superposition der Quellen und kann die Spannung bestimmt werden.

Zunächst wird die Spannungsquelle zu null gesetzt.

Die Teilspannung berechnet sich nach der Spannungsteilerregel zu

Die zweite Teilspannung resultiert aus der Bedingung .

Beide Teilspannungen werden zur Knotenspannung addiert.

Die Gleichungen für und werden nach der zu Beginn aufgestellten Maschengleichung gleichgesetzt.

Da eine Gleichung für den Ausgangsstrom gefordert ist, wird die Spannung ersetzt.

Ein Maschenumlauf ergibt:

Umstellen nach Uop und Ersetzen der Spannung durch das ohmsche Gesetz führt zu:

Eingesetzt in die Gleichung sowie mit dem Zusammenhang wird diese zu:

Die Gleichung wird geordnet.

Auf den ersten Blick erscheint die Gleichung nicht unabhängig von der Ausgangsspannung, wie dies in der Aufgabe beschrieben ist.

Bei genauerem Hinsehen fällt allerdings auf, dass mit und der Ausdruck in der Klammer zu null wird und die Ausgangsspannung damit entfällt.

Ebenso wird der Ausdruck in der Klammer zu null, wenn für die Widerstände und gilt.

In diesem Fall vereinfacht sich die Gleichung für den Ausgangsstrom zu

Der Strom I Aus ist unabhängig von der Spannung

Das bedeutet, dass der Ausgangsstrom unabhängig von der anliegenden Ausgangsspannung fließt.

Es handelt sich um eine ideale Stromquelle.

b) Dimensionieren der Schaltung

Damit der Widerstand bestimmt werden kann, wird anhand der Bedingungen bis und die Spannung über diesem berechnet.

Um den Fehler so gering wie möglich zu halten, werden die maximalen Werte für und verwendet.

Zur Berechnung der Widerstände wird gewählt.

Mit und ergibt sich die Bedingung für die Widerstände und

beziehungsweise

Lösung:

  2. ,
    ,