Aufgabenstellung:
Nutze den Satz von Stokes zum lösen des Oberflächenintegrals:
Hinweis: Der Normalenvektor
Lösungsweg:
Schreibe das Integral mit dem Satz von Stokes um:
Die Idee hinter der Verwendung des Satzes ist die folgende. Es gibt oft den Fall, dass ein Oberflächenintegral berechnet werden muss. Da die Berechnung eines solchen Integrals aber meist alles andere als trivial ist, nutzt man den Satz von Stokes und umgeht damit die komplizierte Rechnung. Statt des Oberflächenintegrals muss anschließend lediglich ein leichter zu lösendes Kurvenintegral berechnet werden.
Zur Berechnung müsst du dir jetzt Gedanken über die Orientierung und den Tangengtenvektor machen:
Die in der Aufgabenstellung gegebene Fläche
Die Umlaufrichtung könntest du nun wie folgt finden. Stell dir vor du seiest der Normalvektor
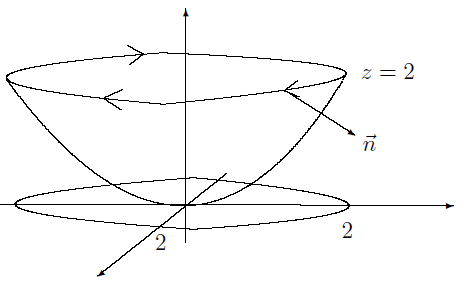
Schaut man sich nun also den Rand an, so geht es um einen Kreis mit dem Radius
Es bieten sich Polarkoordinaten an:
mit
Nun kannst ud das Integaral bestimmen. Achte allerdings darauf, das du wegen der Umlaufrichtung von
Nutze außerdem