Aufgabenstellung:
Gegeben ist ein Vektorfeld
- Berechne das Integral
- Bestätigen dein Ergebnis aus 1. mit Hilfe des Satzes von Stokes.
Lösungsweg:
Es kann helfen zunächst eine Skizze anzufertigen:
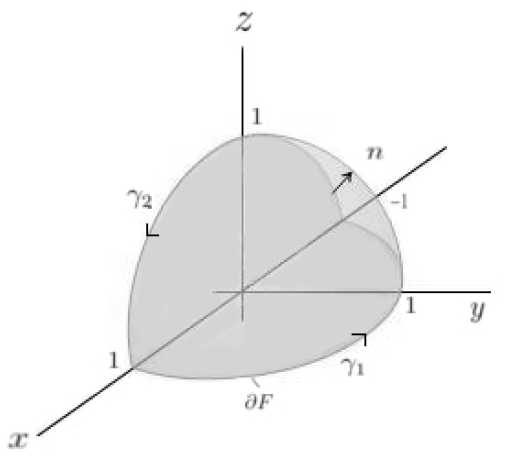
1. Integral:
Parametrisiere die Fläche
Nutze Kugelkoordinaten mit
Aus den Bedingungen in
Daraus folgt weiter:
Berechne die Rotation von
Berechne
Hier zeigt der Normalenvektor nach außen.
Berechne nun das Integral
2. Bestätigen mit Stokes
Parametrisiere die Kurve (bzw. den Rand)
Da der Normalenvektor von
Kurve in der
Kueve in der
Berechne nun das Integral
Lösung:
Sowohl bei 1. als auch 2. erhält man als Ergebnis