Aufgabenstellung:
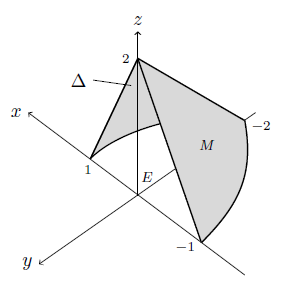
Gegeben ist der rechts abgebildete elliptische Halbkegelstumpf
Weiter besteht der orientierte Rand
Berechne:
- Die Divergenz des Vektorfeldes
mit - Die nach außen weisenden Normalenvektoren
von und von . - Die Flussintegrale
und - Den Fluss
des Feldes durch den Mantel mit Hilfe des Integralsatzes von Gauß und der Ergebnisse aus 3.
Lösungsweg:
1. Berechne die Divergenz von
2. Bestimmung der Normalenvektoren:
Für den Boden gilt:
Der Boden
Stelle eine passende Parametrisierung
Bilde
Bestimme nun
Rechne analog für das Dreieck
Das Dreieck
Parametrisierung von
Dieser Vektor ist schon normiert zeigt jedoch nicht nach außen.
3. Berechnung von
4. Berechnung von