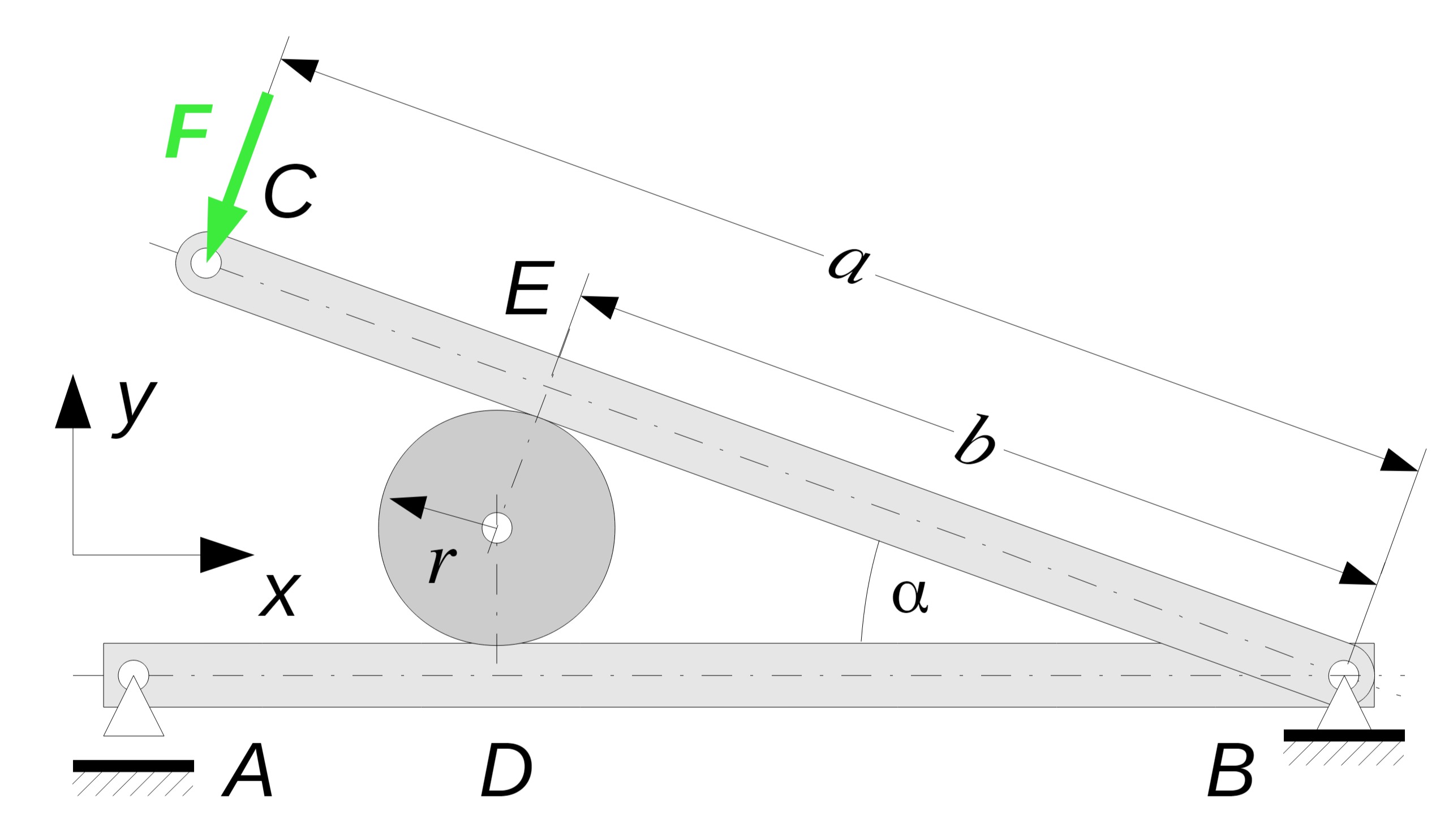
Aufgabenstellung:
Der abgebildete Nussknacker besteht aus den Trägern
- Ermitteln Sie die Länge
- Ermitteln Sie die Kräfte in den Punkten
und . - Wie groß darf der Winkel
höchstens werden, damit die Nuss nicht aus dem Nussknacker rutscht?
Gegeben:
Hinweis:
Lösungsweg:
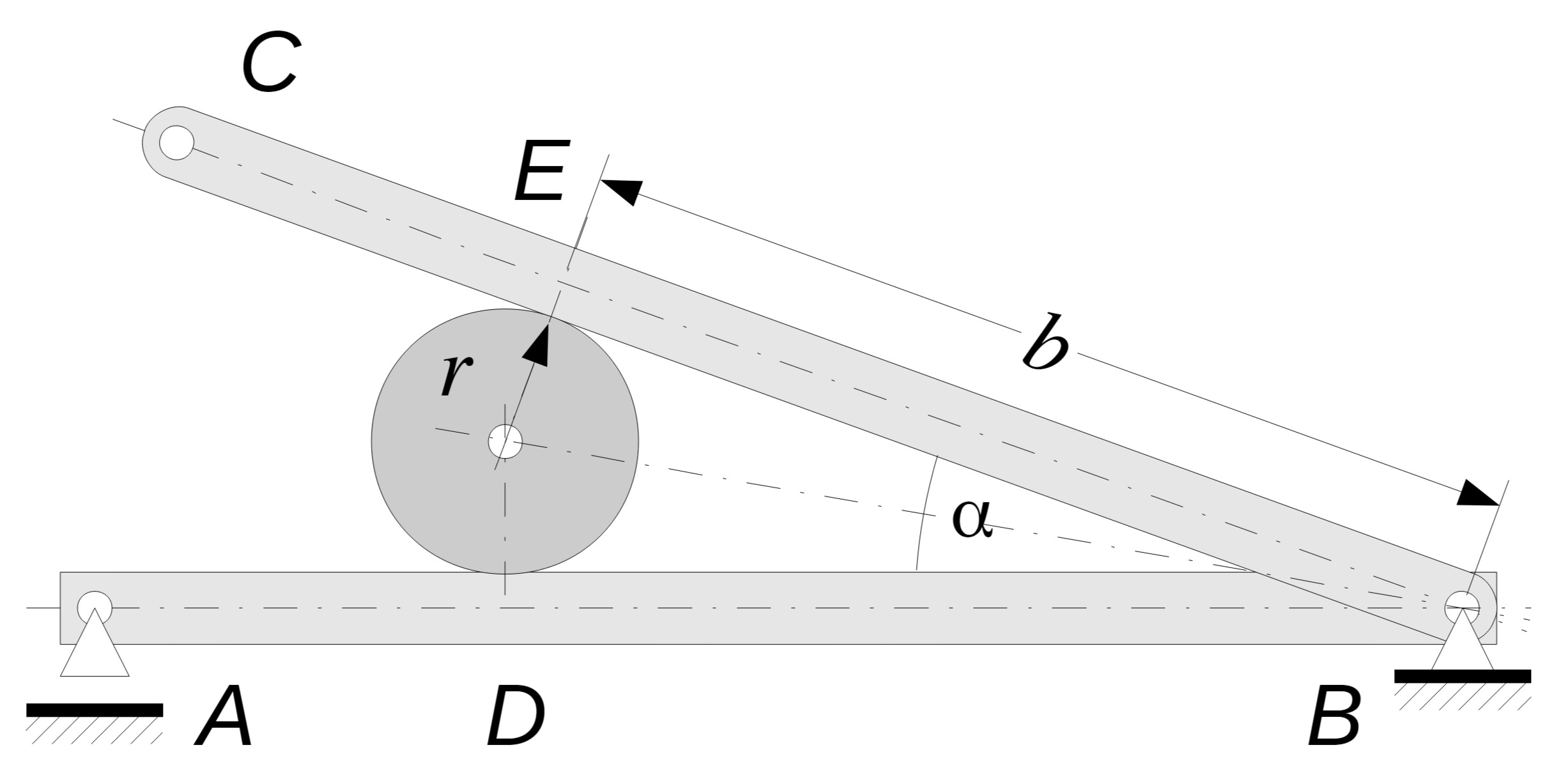
a) Geometrie
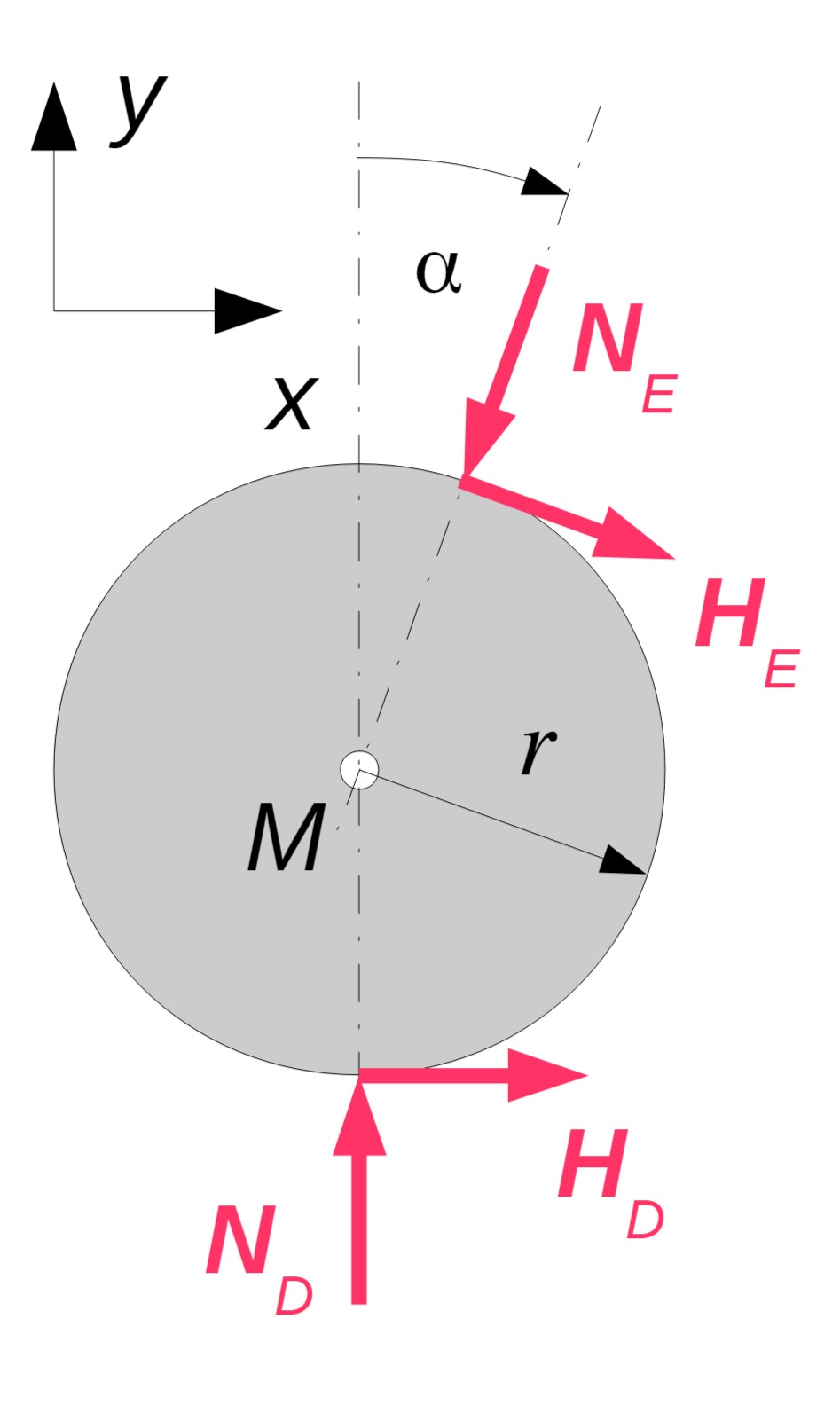
b) Kräfte auf die Nuss
Kugel freischneiden und Gleichgewichte formulieren:
Träger BC:

Aus den Gleichungen ergibt sich:
c) Bedingung für Winkel
Die Kräfte sind in beiden Kontakten gleich. Daher genügt die Betrachtung von einem Kontakt.
Haftbedingung für Punkt
Einsetzen der Kräfte ergibt: