Aufgabenstellung:
Ein Seil hängt zwischen zwei gleich hohen Auflagern und wird durch eine Dreieckslast mit der maximalen Amplitude
Zu bestimmen sind die Seilkraft im Tiefpunkt des Seiles und die Form der Seilkurve.

Lösungsweg:
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen
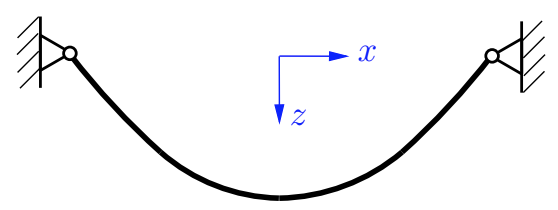
Mit der Wahl des Koordinatensystems in der Feldmitte ergibt sich die Belastung zu
Aufstellen der Selkurve:
Die zweifache Integration der Differentialgleichung der Seilkurve liefert
Aus den Randbedingungen folgen die Integrationskonstanten:
Die Seilkurve lautet somit (Symmetrie!)
Den Horizontalzug
Damit ergibt sich die Seilkraft